『ｆ(ｆ(ｘ))』解答

◆東京都　四年寝太郎　さんからの解答。

●ｆ(ｘ)＝１　 (ｘ＝１の時)

●ｆ(ｘ)＝ ｘ＋１
２
　 (0＜x≦ 1
2		 ,x＝ 1
n		 となる自然数nが存在する時)

●ｆ(ｘ)＝ｘ＋ １
２
　 (0＜x＜ 1
2		 で上の条件を満たさない時)

●ｆ(ｘ)＝ １／ ２(ｘ− １
２		 )
　 ( 1
2		 ＜x＜1,x＝ 1
2		 ＋ 1
2n		 となる自然数nが存在する時)

●ｆ(ｘ)＝１／(ｘ− １
２		 )
　 ( 1
2		 ＜x＜1で上の条件を満たさない時)

●ｆ(ｘ)＝ ２ｘ
ｘ＋１
　 (２≦ｘ＜∞,ｘ＝ｎとなる自然数ｎが存在する時)

●ｆ(ｘ)＝２／( ２
ｘ		 ＋１)
　 (２≦ｘ＜∞で上の条件を満たさない時)

●ｆ(ｘ)＝ ２
ｘ		 −１
　 (1＜ｘ＜2, 1
x		 − 1
2		 ＝ 1
2n		 となる自然数nが存在する時)

●ｆ(ｘ)＝ １
ｘ		 − １
２
　 (１＜ｘ＜２で上の条件を満たさない時)

とｆ(ｘ)を定義すると、
ｆ（ｆ（ｘ））＝ １
ｘ		 となる。

条件を満たす数の推移

１
５		１
４		１
３		１
２
↓↓↓↓
３
５		５
８		２
３		３
４
↓↓↓↓
５４３２
↓↓↓↓
５
３		８
５		３
２		４
３
↓↓↓↓
１
５		１
４		１
３		１
２

◆神奈川県　いわし　さんからのコメント。

四年寝太郎さんの解答へのコメントです。
x= 5
6		 のとき、
1
2		 ＜ 5
6		 ＜１,
5
6		 - 1
2		 = 1
3

ですから、5番目の定義式により
f( 5
6		 )=1/( 5
6		 - 1
2		 )=3 です。

すると、6番目の定義式により
f(f( 5
6		 ))=f(3)= 3
2		 ≠ 6
5

ですから、このxは反例になってしまいます。

◆東京都　元吉　さんからの解答。

x＝1のときf(x)=1

1＜ｘ≦２のときf(x)=2x

２＜ｘ≦４のときf(x)= 2
x

４＜ｘ≦８のときf(x)=2x

８＜ｘ≦１６のときf(x)= 2
x

・・・・・・・・・
・・・・・・・・・

1
2		 ≦ｘ＜１のときf(x)= x
2

1
4		 ≦ｘ＜ 1
2		 のときf(x)= 1
2x

1
8		 ≦ｘ＜ 1
4		 のときf(x)= x
2

1
16		 ≦ｘ＜ 1
8		 のときf(x)= 1
2x

・・・・・・・・・
・・・・・・・・・

【コメント】

これは２がベースになっていますが、いろいろな数のバージョンができそうですね。

◆神奈川県　いわし　さんからの解答。

nを自然数とし、
区間An , Bn , Cn , Dn を

An=(2n−1 , 2n] , Bn=(2n , 2n＋1] ,

Cn=[ 1
2n		 , 1
2n−1		) , Dn=[ 1
2n＋1		 , 1
2n		 )

関数 f : R+→R+ を

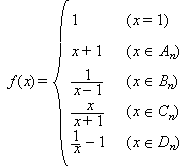
により定義すれば、このfは題意を満たします。

x∈Anはfによって、
An→Bn→Cn→Dn→An と循環します。(下図)

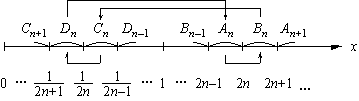
どういう方針で探したかというと、まず
f(1)=1,
a≠1 ⇒ f(a)≠a,
f(a)=f(b) ⇒ a=bです。

R+から1を除いた集合をR1とします。

f(a)=b (a , b∈R1 , a≠b) とすると、aはfによって

a → b → 1
a		 → 1
b		→ a
と循環します。

また、
a, b, 1
a		 , 1
b		のうち

2個は R＋=(1, ∞) に、
他の2個は R−=(0, 1) に含まれます。

そこで、まず R＋, R− に2個ずつ対応する区間を取ります。
(x∈An ⇔ 1/x∈Cn ,
x∈Bn ⇔ 1/x∈Dn となるように、
x∈R1がどれかの区間に属するように)

次に、対応する区間の間でxが循環するようにfを定めます。
上の例では、まず f : An→Bn を
f(x)=x+1 としました。
あとは、いもづる式に決まります。

各区間の境界は上の例に限りませんし、
f : An→Bnも、1対1の、上への関数であれば何でもいいと思います。
もちろん、他の区間のfを先に決めても構いません。

実は、Qを正の有理数全体の集合として、
f : Q→Q ならば、
0＜q＜1, q∈Q なる q に通し番号をつけて
q1 , q2 , …とし、

f(q2n−1)=q2n ,
f(q2n)= 1
q2n−1		 ,

f( 1
q2n−1		 )= 1
q2n		 ,

f( 1
q2n		 )=q2n−1,

f(1)=1 (nは自然数)とすればよさそうだけど、実数の場合はどうしたらいいのか悩んでいたのですが、四年寝太郎さんの解答を見て、無限個の区間に分けることを思いつきました。

◆愛知県　Y.M.Ojisan　さんからの解答。

奇をてらった方法ですが、基本はＦを複素数まで拡張した場合の簡単な解

　F(x) = exp(i*ln(x)) i:虚数単位

を無理やりＲ+に押し込めるものです。

x∈Ｒ+ のとき　y=ln(x)とする。
このとき　ｙ∈Ｒである。

yを論理３進数で表したときの３のk乗の桁値をＹ[k]とする。

これを２桁ずつ区切って、次のように90度回転交換(変換をIで表す)してできた論理３進数をy'とする。
すなわち

　Ｙ'[2j]=Ｙ[2j+1] , Ｙ'[2j+1]=−Ｙ[2j]  j=-∞〜∞整数
ここで論理３進数とは 通常の３進数では各桁値は０又は１又は２であるのに対して、
−１と０と１を使ったものとします。
（±記号が不要になるという特徴をもっています。
また、桁値は−１〜１なので　-1倍したものも、論理３進数の桁値になります。参考参照）

具体的に書くと

y = abcd.efgh....  → I(y)=y'=b(-a)d(-c).f(-e)h(-g)....∈Ｒ
このy'を用いて　F(X)=exp(y')とする。

このとき　
F(F(X))
= exp( I( log(exp(y')) )
=exp(I(y'))
=exp(-(abcd.efgh....))
=exp(-log(x))
=1/x　で条件を満足する関数です。

【参考】

x:10進x:論理３進表記
(-1:N 0 1)		I(x)10進
-4NN-2
-3N01
-2N14
-10N-3
0000
1013
21N4
310-1
4112

【どんな形か】

いたるところ連続でないので、プロットして見るとおもしろい。
VBの関数を添付します。

Function F(x As Double) As Double
  F = Exp(論理3進To10進(I変換実行(論理3進化(Log(x)))))
End Function

Function 論理3進化(x As Double) As String
    N = Application.Max(0, Int(Log(Abs(x) + 1E-16) / Log(3) + 1))
    If N Mod 2 = 0 Then N = N + 1
    論理3進化 = ""
    Pn = 3 ^ N
    Px = x
    For i = N To N - 33 Step -1
       Yi = Px / Pn
       Yi = Switch(Yi > 1.5, Yi, Yi >= 0.5, 1, Yi > -0.5, 0, Yi >= -1.5, -1, 1, Yi)
       
       論理3進化 = 論理3進化 & Switch(Yi = 1, "1", Yi = -1, "N", Yi = 0, "0", 1, "?")
       If i = 0 Then 論理3進化 = 論理3進化 & "."
       Px = Px - Pn * Yi
       Pn = Pn / 3
    Next i
End Function

Function 論理3進To10進(x As String) As Double
    N = InStr(x, ".") - 2
    論理3進To10進 = 0
    Pn = 3 ^ N
    j = 1
    For i = 0 To 32
       If i = N + 1 Then j = j + 1
       Yi = Mid(x, j, 1)
       Yi = Switch(Yi = "1", 1, Yi = "0", 0, Yi = "N", -1)
       論理3進To10進 = 論理3進To10進 + Pn * Yi
       Pn = Pn / 3
       j = j + 1
    Next i

End Function

Function I変換実行(x As String) As String
    N = InStr(x, ".") - 2
    I変換実行 = ""
    j = 1
    For i = 0 To 33 Step 2
       If i = N + 1 Then j = j + 1: I変換実行 = I変換実行 & "."
       Yia = Mid(x, j, 1)
       Yia = Switch(Yia = "1", "N", Yia = "0", "0", Yia = "N", "1", 1, "?") ' "-ya"
       j = j + 1
       
       If i = N Then j = j + 1:   I変換実行 = I変換実行 & "."
       Yib = Mid(x, j, 1)
       j = j + 1
       Pn = Pn / 9
       I変換実行 = I変換実行 & Yib & Yia
    Next i
End Function
【例】 
X　0.1
ln(X)　-2.302585092994050
y(論理3進表記）　N1.N01N1111N1N00N0N0N10N100N0N00110
y'=I(y)(論理3進表記）　11.01NN1N1N1101N0N0N00N11000101100N
再10進化　4.06484563
F(X)=exp(I(y'))　58.25591475

【コメント】

この方法は一見解のようにみえますが、実は不正解だそうです。
どうして不正解なのかを問題にしますので、解答をお寄せください。

ヒント　0.5=0.49999....................

◆東京都　建築家　さんからの解答。

(logX)を一番上から５桁目の数字が偶数の場合は一つ大きな奇数に、
奇数の場合は一つ小さな偶数に交換した値になるような(logX')があった時に
(logX)の上から５桁目が

　偶数の場合は　　f（X）＝X’
　奇数の場合は　　f（X）＝ １
X’

ただしX=1の場合に限り
f(1)=1とすればこのf(X)は題意をみたします。

【追加問題解答】

まず、a≠bの時にf(a)≠f(b)となり、
f(x)＝N　(N∈R+)となるxが存在すると仮定すると
f(f( 1
N		 ))＝f(x)＝N　( 1
N		 ∈R+) で矛盾

つまりf(x)は全単射な関数であることに注意する。

Y.M.Ojisanさんの方法によるとこの全単射が至る所でくずれている箇所が存在します。
ヒントにあるような例で論理３進表記すると。

N0.1N1N1N1N1N1N・・・ ≠   11.0000000000・・・
　　　↓　　　　　　　　　　　　　↓
01.NNNNNNNNNNNN・・・ ＝   1N.0000000000・・・
　　　↓　　　　　　　　　　　　　↓
10.N1N1N1N1N1N1・・・ ≠   NN.0000000000・・・
という部分で矛盾ができます。

I(x)の表を見たときにあれと思ったのですが、00→00が原因でしょう。
循環が均一でないようです。
これはおそらくx＝1付近での収め方の為にこのようにしたのだと思われます。
連続でない写像の場合はこの辺が難しいですね。

いわしさんの言うように、区間内全単射の半開区間（といってもこの場合は循環区間のペアでしょうか）を １に近づくにつれ細かく無限個に刻むのがよいと思います。
つまり３進数ではなく２進数で十分ではないでしょうか。

先程の、上から５桁目の・・・は大丈夫ではないかと。
言葉でいうと簡単ですが「一番上から○桁目」というのがポイントでしょうか。
要は１０nで細かく分割してることになります。

◆東京都　建築家　さんからの解答。

f(x)が満たさねばならないような条件を示しておきます。

f(1)=Nとするとf(N)=f(f(1))=1なのでf(f(N))=f(1)= 1
N

∴N=1　つまりf(1)=1

f(a)=aとするとf(f(a))=f(a)= 1
a
∴a= 1
a		 　つまりa=1

f:R+→R+　は全単射である。

1の近くで連続であるとすると、あるaで
1
a		 ＜1＜aでf(x)が連続でf(1
a		 )＜f(1)＜f(a)とする。

1
a		 ＜1
b		 ＜1＜b＜aとなるようなbの全ては
f(1
b		 )＜1＜f(b)

一方 1
a		 =f(f(a))＜1＜f(f(1
a		 ))=a

今bの中にf( 1
a		 )＜1
b		 ＜1＜b＜f(a)を満たすものが存在するが
f(b)＜1＜f( 1
b		 )で矛盾。

不等号が逆でもいえるので、f(x)は1の付近では連続ではない。

ここでR+×R+平面上にあるこの関数を対数を使ってR×R上に写すと分かりやすいです。

log・f・{log-1}＝g , logx=t と置くと
g(g(t))=log(f(f(x))=log( 1
x		 )=-logx=-t

また上からg(0)=0,g(a)=aならばa=0,gは全単射、が言える。

-g(-・)=h(・),-t=u　とするとh(h(u))=-g(g(t))=t=-u
となることからg(t)は原点に点対称な関数である。

全単射なのでg-1が存在して g(t)=g-1(-t)となるので
g(t)は原点を中心に90度回転させて一致する。

とここまでくると対称性があってf(x)よりは見通しがよいのではないでしょうか。
写像gによって(t,g(t))の点は第１〜４象限を巡回します。

つまりこの平面においてR+を二つの集合にわけてそれを入れ替えるような写像を考えれば、
R+,R-の四つの集合ができて、それを巡回するような写像gはすぐ見つかりますので
最後にf(x)の式に還元すればよいことになります。

　『ｆ(ｆ(ｘ))』へ

　数学の部屋へもどる