ですから隣の車の１７．５リットルのガソリンをもらっても、１９．５リットルで次の車に到達することはできません。
ただし２１．５→２１．５→１７．５→・・・と進めば１周できます。
◆広島県 清川 育男 さんからの解答。
【問題１】
条件２，３から、Ｅ，Ｆ，Ｇは同じ車に乗ることになる。
条件１，２，３から
1) （Ｃ，Ｅ，Ｆ，Ｇ）,（Ｄ，...）
2) （Ｃ，...），（Ｄ，Ｅ，Ｆ，Ｇ）
１），２）の２つの場合がある。
条件４から１）の場合は不適合。
したがって条件１，２，３，４を満たす乗り方は
（Ａ，Ｂ，Ｃ），（Ｄ，Ｅ，Ｆ，Ｇ）となる。
Ｂ子さんはＡ夫，Ｃと同乗することになる。
【コメント】
この問題は、清川さんには簡単すぎたかもしれません。
追加の問題を考えているので、しばらく待ってくださいね。
◆広島県 清川 育男 さんからの解答。
【問題２】
Ｎ台の車が停車しているとする。
環状の道路であるから、Ｎ区間に分割される。
その全ての区間がつながる車とガソリンの位置関係にあれば、かろうじて可能となる。
その確率は、１／２N。
この位置関係にあれば、Ｎ台の車の１つは可能となる。
したがって、Ｎ／２Nの確率で１台の車が１周出来る。
停車している車が多い程、その確率は少なくなる。
答え Ｎ／２Nの確率で１台の車が１周出来る。
【コメント】
問題の意味が分かりにくかったと思いますが、ガソリンをもらうことを認めると、実はＮ台の車の中には必ず一台は１周できる車が存在します。
そのことを証明してください。
◆広島県 清川 育男 さんからの解答。
【問題２】
ランダムに考えて、確率の問題にすり替えてしまいましたが、問題の意味がわかりました。
Ｎ台停車している車のなかで「残りのガソリンが一番多い車」は「問題の条件」からその前に停車している車までたどり着くことが出来る。
そこでその車に残っているガソリンを全部もらって、さらに前進する。
このように次々に前に停車している車から全部のガソリンをもらうことが出来れば、かろうじて、一周出来ることになる。
【コメント】
反例を作りました。
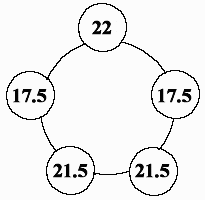
例えば、５台の車があり、１周に１００リットルが必要であるとします。
５台の車は環状に等間隔に並んでおり、ガソリンの量は順に、
２２，１７．５，２１．５，２１．５，１７．５
であったとしましょう。
残りのガソリンが一番多い車は２２リットルの車ですが、２０リットル費やして隣の車に到達した後は、２リットルしか残りません。
ですから隣の車の１７．５リットルのガソリンをもらっても、１９．５リットルで次の車に到達することはできません。
ただし２１．５→２１．５→１７．５→・・・と進めば１周できます。
◆広島県 清川 育男 さんからの解答。
【問題２】
反例であげられた、２２，１７．５，２１．５，２１．５，１７．５について。
車を順に１番、２番、３番、４番、５番とすると
上記の場合は３番の車が可能ですね。
停車している車をＴ台，１周するのに要するガソリンをＭリットルとしたとき、それぞれＴ台の車のガソリンの量を
１）Ｔｎ＜Ｍ／Ｔ
２）Ｔｎ＝Ｍ／Ｔ
３）Ｔｎ＞Ｍ／Ｔ
（ｎは１からＴまでの自然数）
上記の３つのグループに分ける。
反例の場合は１）２台。２）０台。３）３台。
どの車が可能かの見つけ方は、残りのガソリンが最小の車を探し、
（（１）のグループが２台なので）
それより先行する３のグループが連続して２台（２のグループは無視する）あれば、最小のガソリンの車より先行している最初の車（この場合は３番の車）と言うことになります。
一般的に表現するのに困っています。
最小のガソリンの車を探すのは必須ですが。
【コメント】
具体的な手順を探すのはかなり大変です。
私自身は直接的な証明から逃げて、背理法を使うか、鳩を飛ばすことを考えています。
でも直接の手順を指摘できればベストでしょうね。
◆広島県 清川 育男 さんからの解答。
【問題２】
Ｎ台の停車している車の燃費は同じとする。
簡単にするために、燃費は悪いが１リットルで１ｋｍ走行出来るとする。
環状道路の１周の距離をχｋｍ、ガソリンのトータルをＧリットルとする。
Ｎ台の車をＤ１，Ｄ２，・・・・，Ｄｎとする。
Ｄ１の先行車までの距離をχ１とする。
・・・・・・，
Ｄｎの先行車までの距離をχｎとする。
Ｄ１のガソリンの量をＧ１とする。
・・・・・・，
ＤｎのガソリンをＧｎとする。
χ１＋χ２＋・・・・・＋χｎ＝χ。
Ｇ１＋Ｇ２＋・・・・・＋Ｇｎ＝Ｇ。
（Ｇｎ−Ｘｎ）を車Ｄｎの「ゆとり量」とする。
１）特殊な場合
Ｇ１−Ｘ１＝０，Ｇ２−Ｘ２＝０，・・・・・・，Ｇｎ−Ｘｎ＝０。
この場合はどのＮ台の車も１周出来る。
２）一般の場合
イ）「ゆとり量」がマイナスの車の台数Ｍを調べる。
ロ）Ｇｎ−Ｘｎ（ゆとり量）が最小となるｎを探す。
ハ）その車の先行車から先さきの「ゆとり量」をチェックする。
ニ）「ゆとり量」がマイナスならパス。
ホ）「ゆとり量」がプラスのとき
しかしながら先行車までの距離はどのようにしてわかるのか。
Ｎ台の車のガソリンの残りはどのようにしてわかるのか。
という２点の問題が残るので、そもそもの問題は特殊な場合を除き、必ず１台の車は１周出来ると言う問題になるのではないかと思います。
◆広島県 清川 育男 さんからの解答。
【問題２】
環状道路に燃費が同じＮ台の車が停車しているとする。
背理法による証明を試みる。
仮定Ａ）「少なくとも１台は先行車にたどり着くことが出来るガソリンが残っている。」
Ｎ台すべての車が先行車にたどり着くことが出来ない（そういった距離間隔に停車している）と仮定する。
そうすると、Ｎ台の車の残りのガソリンを足すと少なくとも１台は１周出来るという条件に反する。
したがって仮定Ａは成り立つ。
仮定Ａは成り立ち、かつ、Ｎ台すべての車の車が１周出来ないと仮定する。
そうすると、Ｎ台の車の残りのガソリンを足すと少なくとも１台は１周出来るガソリンの量が残っていることに反する。
したがって少なくとも１台の車は１周出来ることになる。
以上です。
しかしながら、ガソリンがなくなってしまうので、試しに行動することは出来ない。
１周するためには１／Ｎより大きい確率に期待するしかないように思います。
【コメント】
２つ目の仮定から、結論を導くのは少し論理の飛躍があると思うのですが、どうでしょうか。
◆静岡県 ヨッシーさんからの解答。
【第２問】の解答
例えば、ガソリンの量と距離を
| ガソリン量（km換算）： | ３ | ４ | ５ | ３ | ５ |
| 距離(km) ： | ５ | ５ | ５ | ４ | １ |
とします。
ガソリン量と、距離の合計が一致していればどんな数でも良いです。
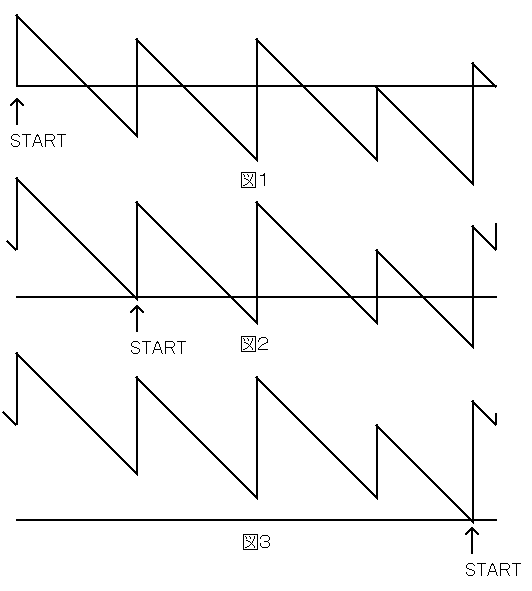横軸に距離、縦軸に残りガソリン量を取ってグラフにすると、図１のように、必ず０で終わるノコギリ型のグラフになります。
どの車を出発点にしても同じです（図２）
このグラフが最小値となる点（複数あればどれでも良い）を出発点にすると図３のように、ガソリンがなくなることなく１周することが出来ます。
【コメント】
グラフを見れば、一目瞭然ですね。
◆兵庫県の中学校３年生 浅田 有貴 さんからの解答。
【問題１】
Ａ夫、Ｂ子、Ｃが乗車する車と、Ｄ，Ｅ，Ｆ，Ｇが乗車する車に分ければいいと思います。
Ｂ子は二人の家族と乗ることになります。
◆千葉県 津田 さんからの解答。
【問題２】
清川さんの『仮定Ａ）
「少なくとも１台は先行車にたどり着くことが出来るガソリンが残っている。」が重要です。
仮定というより補題ですね。
この証明は清川さんが済ませているので省略します。
数学的帰納法で証明します。
台数をｎとして、ｎ＝１のときは明らかに可能です。
ｎまで可能とします。
ｎ＋１のとき、補題より、先行車にたどりつくことができる車が存在します。
それをＡとします。
Ａがたどりつく車をＢとします。
ここで、Ａ，Ｂのガソリンを全てＡに移し、Ｂをなくしてしまった状態を考えますと、これはｎ台の状況ですから、必ず１周できる車が存在します。
その車は元々の状態（Ｂが存在する状態）で当然１周可能です。
したがって、ｎ＋１でも１周可能であり、結局ｎがいくらであっても１周可能です。
（感想）
補題には直ぐに気づきましたし、そうすると帰納法が使えることも直ぐに分かりました。
◆滋賀県の中学校３年生 ００９ さんからの解答。
【問題１】
まず、CとDは、別なので [C] [D]
EとG、Fは一緒だから [E,G,F]
4人までだから、A.Bは、Cと一緒
よって、B子は、２人と乗る。
◆大阪府 はる さんからの解答。
【問題１】
車をそれぞれ１，２と置く。
ＦＧＥを一まとめにして考え、これが１の車に乗るとすると、残りの席は１つしかないので、まずＢかＤと必ず一緒に乗るＡは２の車に乗ることとなる。
そこで、１に乗るのはＢＣＤの誰かとわかる。
次に、Ｂが１に乗るとすると、残りのＣとＤが２に乗ることになるが、二人は仲が悪く別々の車に乗るためＢは２に乗ることになる。ＣとＤではＡはＢかＤのどちらか一方と乗るのでＢが２に乗った場合Ｄは２に乗らないので、車に乗った人達の組み合わせは
１（ＦＧＥＤ） ２（ＡＢＣ）となる。
そこで，Ｂが一緒に乗った人数は２人である。
◆群馬県の中学校２年生 藤咲 洋輔 さんからの解答。
【問題１】
Ｂ子を抜かして２人。
具体的に言うと１台目にＡ，Ｂ，Ｃで２台目にＤ，Ｅ、Ｆ、Ｇとなる。
◆京都府の中学校３年生 ピリカラもっくん さんからの解答。
【問題１】
まず条件1からＣは1の車にＤは2の車に乗るとします。
次に条件2と3からＥとＦとＧは同じ車に乗ることが分かります。
条件4からＢ子とＤは別々の車に乗ることが分かります。
Ｄは2の車に乗っているのでＢ子は1の車に乗ることになります。
この時点で1の車には二人、2の車には一人乗っています。
一台の車に4人しか乗れないのでＥ、Ｆ、Ｇは2の車に乗ることになります。
最後にＡ夫は1の車に乗ることになるので、Ｂ子は二人の家族と一緒に乗ることになる。
◆山梨県 Footmark さんからの解答。
【問題２】
小学生にも理解できるような論理に努めました。
今まで乗っていた車の燃料は次の車に足して次々と車を乗り継ぐこととして証明します。
任意の車を出発点とし、その位置をＰ点とします。
その車から出発しＰ点の一台手前の車にたどり着く前に燃料切れになったら、やむを得ないので先の車まで歩いて行くことにします。
Ｐ点の一台手前の車にたどり着く前に燃料切れになる間はこのことを繰り返します。
すると、いつかはＰ点の一台手前の車に乗る時がきます。
もし仮にこの車がＰ点にたどり着く前に燃料切れになったとするとＰ点まで歩かねばなりません。
すべての車の全燃料を使い切ったにも関わらず歩いた道のりがあるので題意に矛盾します。
それ故、上の方法を採る限りＰ点には必ず車で来ることになります。
Ｐ点に到着した車は、その車の燃料を使い切ってすべての車の全燃料を使い切った事になるので、題意より今まで歩いた距離を走るだけの燃料が必ずなければなりません。
それ故、少なくともＰ点まで乗り継いでいった最初の車は、その車を出発点にすれば間違いなく一周できる筈です。
よって、ある車を出発点とさせることで無事一周できる車は少なくとも一台はあります。
◆岩手県の高校生 からすみ さんからの解答。
【問題１】
まず、２台の車をそれぞれＸ，Ｙとします。
条件１より、Ｘ，Ｙに１人ずつ入ります。
条件２，３より、Ｅ，Ｆ，Ｇは、一まとめとして考えられる。
この時、どちらかの車(仮にＸとする）は、すでに満席となっているはず。
夫は、Ｂ子さんか、Ｄ君と一緒だから、既にお子さんで埋め尽くされているＸ車には乗れない。
よって空きのあるＹ車に、奥さんと一緒に乗り込むことになる。
◆大阪府 fuku66 さんからの解答。
【問題１追加問題】
条件の1,2,3が全て正しいとすると矛盾が生じる。
よって嘘の条件はこの中にある。
1)条件1が嘘の場合。
条件2,3よりEFGは同じ車に乗ることになる。
条件4よりABはEFGと同じ車に乗らなければならない。
さらに条件5よりCDがABEFGと同じ車に乗らなければならない。
これは定員オーバーである為、不適。
2)条件2が嘘の場合。
条件1,3より、EGの乗る車とFの乗る車に分けることが出来る。
前者を車X、後者を車Yとする。
条件6より車XにはEGのほかにBHが乗車している。
条件4より車XにはBHEG、車YにはFAが乗車しなければならない。
条件5より車XにはBHEGD、車YにはFACが乗車している。
車Xの運転席・助手席にBDが座り、後部座席にEGHが座ることで条件は満足される。
（車YはFACが任意の座り方で良い。）
3)条件3が嘘の場合。
条件1,2よりEの乗る車Xと、FGの乗る車Yに分けることが出来る。
条件6より車YにはBFGHが乗ることになる。
条件4より車XにはAEが、車YにはBFGHが乗ると分かる。
条件5より車XにはACEが、車YにはBDFGHが乗ると分かる。
車XはACEが任意の座り方で条件を満たし、
車Yは前部座席にBDが、後部座席にFGHが座れば条件を満足する。