���R�����@Footmark�@����̉B
�y�����z
�����Qq�|�P�@(���͂Q�����̐���)
�y�l�@�z
�`��n�bm*n-m�bk
| �� | ���I ���I���I{���|(���{��)}�I |
| �� | ���I(���{��)�I ���I���I{���|(���{��)}�I(���{��)�I |
| �� | ���I {���|(���{��)}�I(���{��)�I | * | (���{��)�I ���I���I |
�a��m+k�bm
| �� | (���{��)�I ���I���I |
�����ŁA�` �� �a �̋���v���邱�ƂƁA�`�{�a �������ł��邱�ƂƂ͓����ł�����A
�`�{�a
| �� | (���{��)�I ���I���I | [ | ���I {���|(���{��)}�I(���{��)�I | + �P ] |
���C�����Ȃ� ��,k �ɑ��Ă���ɋ����łȂ���Ȃ�܂���B
| �E�ӂ̐ς̍����� | (���{��)�I ���I���I | �́A |
�ł�����A�ς̉E���������ɁA�܂�
| ���I {���|(���{��)}�I(���{��)�I | ���A��Ɋ�łȂ���Ȃ�܂���B |
���{������ (���R���͂O��������)�Ƃ���ƁA
| ���I {���|(���{��)}�I(���{��)�I | �� | ���I (���|��)�I���I | ��n�bp |
���́A�����Ȃ� �� �ɂ����Ă���� n�bp ����ɂȂ� �� ��T�����ƂɂȂ�܂��B
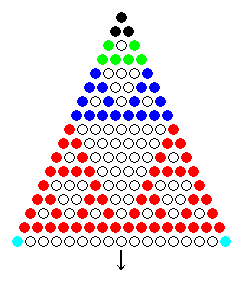
�p�X�J���̎O�p�`�ł́A���P�s�̂��ׂĂ̒l����ł���i��T�����Ƃł��B
�P�ԏ�� 0�b0���P �������A�����(�F�����܂�)�A�������� �ŕ\�����p�X�J���̎O�p�`�͈ȉ��̂Ƃ���ł��B

���̎O�p�`�ŁA���P�s�̂��ׂĂ̒l����Ȃ̂́A�P�ԏ�́��_�ɂ��ā�(�F�����܂�)�̐��łł���O�p�`�̒�ӂł��B
���炩�ɁA��ӂ� �Qq �i�ڂɓ�����܂��B�i���͂P�����̐����j
�Ƃ��낪�A�P�ԏ�ɂ� 0�b0���P �������Ă܂����A�܂� �Q���� �ł��B
���@�����Qq�|�P�@�@(���͂Q�����̐���)
�y�o�E�r�z
�ƂĂ��A�ʔ�����肾�Ǝv���܂��B
����錧�@����@�N�K�@����̉B
������ʉ����Ĉ�ʂ̑f��p�ōl����B
A=nCm*n-mCk�CB=m+kCk �Ƃ����܂��B
�C�ӂ�0�ȏ�̐���m�Ak�ɑ��āA
A��p�Ŋ�����B�� B��p�Ŋ�����B
�ƂȂ�悤�ȁAn��m+k�ƂȂ�悤�Ȏ��R�������߂�B
�y�����z
n=pf*t-1
�������Af��0�ȏ�̐����At��p-1�ȉ��̎��R��
�y�z
�܂��Ap�Ŋ����Ȃ����R��x�ɑ��āAxp-1��1 (mod p)�ƂȂ�B
�ؖ��́A������Hpart2���Q�Ƃ��������B
����Ax��p�Ŋ�����Ƃ��A
�@xp-1��0 (mod p)
A�AB����p�Ŋ����Ȃ��Ƃ��A
�@Ap-1-Bp-1��1-1��0 (mod p)
A�AB����p�Ŋ�����Ƃ��A�@
�@Ap-1-Bp-1��0-0��0 (mod p)
����āAAp-1-Bp-1��0 (mod p)�ƂȂ�悤�ȁAn�����߂�悢�B
A=nCm+k*B �Ə�����̂ŁA
0��Ap-1-Bp-1
��Bp-1*(nCm+kp-1-1)
B��p�Ŋ����Ȃ����Ƃ�����̂ŁA
nCm+kp-1-1��p�Ŋ�����B
nCm+kp-1��1 (mod p)
�܂�A0��j��n�����C�ӂ�j�ɑ��āAnCj��p�Ŋ����Ȃ������K�v�\�������ł��B
�����ŁA�L���̒�`�����܂��B
���R��d�ɑ��āAd���Aph�Ŋ����Aph+1�Ŋ����Ȃ��Ƃ��A
h=l(d)�Ə������Ƃɂ���B
�������Ad��p�Ŋ����Ȃ��Ƃ��Ah=0�ƍl����B
�܂��A���̂Ƃ��Ad=ph*s
�@s��p�Ŋ����Ȃ����R���Ə�����B
0�ȏ�̐���f���Af=l(n+1)�Ƃ����A
����ƁAn+1�́An+1=pf*t
�@t��p�Ŋ����Ȃ����R���Ə�����B
�����ŁA���̂��Ƃ�������B
�y�P�z
t��p�ƂȂ�Ƃ��A![]() ��p�Ŋ�����B
��p�Ŋ�����B
�y�ؖ��z
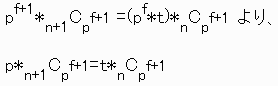
t��p�Ŋ����Ȃ��̂ŁA1�D���������B
�ؖ��I
�y�Q�z
t��p�ƂȂ�Ƃ��A�C�ӂ�0��j��n�ƂȂ�j�ɑ��āAnCj��p�Ŋ����Ȃ��B
(t��p�ƌ݂��ɑf�Ȃ̂ŁAt=p�Ƃ͂Ȃ�Ȃ�)
�y�ؖ��z
j��1�̂Ƃ�
| nCj= | (pf*t-1)*(pf*t-2)*���(pf*t-j) 1*2*���*j | �ƂȂ�B |
1��r��j�Ȃ�C�ӂ�r�ɑ��āA
r��j��pf*t��pf+1������Al(r)��f+1�A
�����l(r)��f�ƂȂ�B
v=l(r)�Ƃ���ƁAr=pv*w�Aw��p�Ŋ����Ȃ����R���Ə�����B
v��f�̂Ƃ��A
pf*t-pv*w=pv*(pf-v*t-w)
pf-v*t-w��-w (mod p)
������A
pf-v*t-w��p�Ŋ����Ȃ��B
l(pf*t-r)=v=l(r)
v=f�̂Ƃ��Apf*w=r��j��pf*t-1��pf*t
����āAw��t�ƂȂ�B
pf*t-pv*w=pf*(t-w)
1��t-w��p������t-w��p�Ŋ����Ȃ�
l(pf*t-r)=v=l(r)
����āA
l(nCj)
| = | j �� r=1 | {l(pf-r)}- | j �� r=1 | l(r) |
| = | j �� r=1 | l(r)- | j �� r=1 | l(r) |
| =0 |
nCj��p�Ŋ����Ȃ��B
j=0�̂Ƃ��AnC0=1�͖��炩�ɁAp�Ŋ����Ȃ��B
����āA��ӂ͌������B
�ؖ��I���B
����āA0��j��n�����C�ӂ�j�ɑ��āAnCj��p�Ŋ����Ȃ�n�́A
0�ȏ�̐���f�ƁAp-1�ȉ��̎��R��t�ɂ���āA
n=pf*t-1�Ƃ��������o����n�Ɍ���܂��B
�I���
�y���܂��z
���̂Ƃ��A
nCm*n-mCk=nCm+k*m+kCk������A
l(nCm)+l(n-mCk) =l(nCm+k)+l(m+kCk)�ƂȂ�B
l(nCm)=l(nCm+k)=0�ƂȂ�̂ŁA
l(n-mCk)=l(m+kCk)
�ƂȂ�B
���l�ɂ��āAl(n-kCm)=l(m+kCm)
����āAm+kCk=m+kCm���
l(n-mCk)
=l(m+kCk)
=l(n-kCm)
=l(m+kCm)
����ɁAn-mCk=n-mCn-m-k
n-kCm=n-kCn-k-m����A
l(n-mCk)
=l(m+kCk)
=l(n-kCm)
=l(m+kCm)
=l(n-mCn-m-k)
=l(n-kCn-k-m)
�������܂��B
�@�w�R���r�l�[�V���� Part2�x��