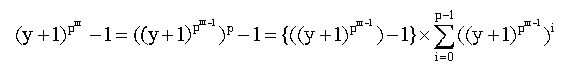
◆愛知県 Y.M.Ojisan さんからの解答。
【定理1≒アイゼンシュタインの定理】
xの整数係数m次モニック多項式A(x)があって、A(0)=p:素数であり、かつm次を除く係数が全てpの倍数であるとき、
A(x)は整数係数の範囲では因数分解できない。
∵ A(x)が因数分解できるとすると、m=b+c (b>0 c>0 整数)として、次のように因数分解される。
| A(x)=(±xb+ | b-1 Σ i=1 |
Bixi | +1)(±xc+ | c-1 Σ i=1 |
Cixi | +p) |
xの整数係数モニック多項式A(x)、B(x)、C(x)があって、A(x)=B(x)C(x)である。
また、A(x)とB(x)の最高次数を除く項の係数が素数pの倍数であるとき、
C(x)の係数もまた、最高次数を除く項の係数が素数pの倍数である。
∵
A(x)=xb+c+pA’(x)、
B(x)=xb+pB’(x)、
C(x)=xc+C’(x) とする。
A(x)=B(x)C(x)に代入して計算すると
xbC’(x)=p(A’(x)−B’(x)C’(x)−B’(x)xc)
である。
よってC’(x)の係数はpの倍数である。
| (y+1)p−1=y× | p-1 Σ i=1 |
pCi+1yi |
であるので少なくとも2個に因数分解できる。
Σのある方の因数の係数は pCi+1であり、pが素数なので、
最高次数yp-1の係数が1(モニック)であることを除き、pの倍数である。
また、0次の係数はpC1=pである。
よって定理1によりこれ以上因数分解できない。
【命題2】
pkの約数の数はk+1である。
命題1同様に x=y+1 と置き換え yの整式にして、数学的帰納法で証明する。
k=1の場合は命題1により成立している。
k=m−1のときに成立しているとする。
即ちm個に因数分解されるとする。
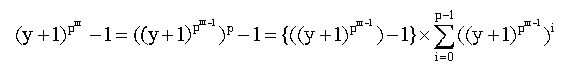
である。前方の因数は仮定によりm個に因数分解される。
よって後方Σのある項がこれ以上因数分解できないことを証明できれば良い。
ところで一般に Q=pm に対して
QCi はi=0、Qを除いてpの倍数である。
従って、(y+1)Q−1 も (y+1)Q/p−1 も 最高次数以外の係数がpの倍数である、モニックである。
よって定理2により、後方Σのある項も最高次数以外の係数がpの倍数である、モニックである。
またその0次の係数は y=0を代入することによりpであることがわかる。
即ち定理1によりこれ以上因数分解はできない。
【命題3】
(1)p=2 のとき 2pkの約数の数はk+2である。
一方命題2より因数分解の数はk+2である。
(2)p≠2 のとき、即ち奇数のとき、2pkの約数の数は2(k+1)である。
式を変形するとpが奇数なので下記である。
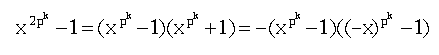
従って、命題2より因数の数は2(k+1)である。
以上より因数の数は2pkの約数の数であるといえる。
【命題4】
xn-1 を複素数の範囲で因数分解すると下記である。
| xn-1= | n-1 Π k=0 |
(x−exp( | 2πi n |
)) |
| n/q-1 Π k=0 |
(x−exp( | 2πiq n |
))=xq−1=(x−1)(xq-1+・・・+1) |
従って、(x−1)をq=1に対応させれば、少なくともnの約数の数だけ因数の種類が存在していることがわかる。
(注記:ただしこれは因数の種類の数であり、因数分解した因数の数ではない。
たとえば3個に因数分解される場合、因数の種類数は最大7個である。)
nの約数q1とq2の最小公倍数Lがn未満のとき、Lはnの約数である。
即ち、q1、q2に対応する因数は、Lに対応する因数を共通因数として持っている。
従って、因数の種類を q1、q2、L対応の3個からより因数に近い
q1対応因数/L対応因数 、q2対応因数/L対応因数 、L対応因数
の3個に置き換えることができ、その数は同じである。
以上から、xn-1
を因数分解したときの因数の数は、少なくともの約数の数になることがわかる。