『高校生からの挑戦状Part25』解答

◆神奈川県　泥棒 さんからの解答。

【（a）〜（c）について】

一辺がnの立方体において、立方体の頂点を含む単位立方体を一つ選ぶ。
（立方体の8隅のうち一つを選ぶ。）

次に、その単位立方体を含んだ、立方体の対角線上にある単位立方体を順に選ぶ。
（n個の単位立方体を選んだことになる。）

そうすると、n³個の単位立方体のどれを選んでも、問題文の操作によって引かれた直線の少なくとも一本が貫通する。

◆愛知県　YMOjisan さんからの解答。

【a-bの解答】

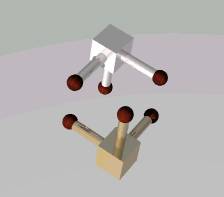
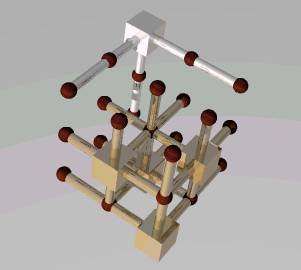
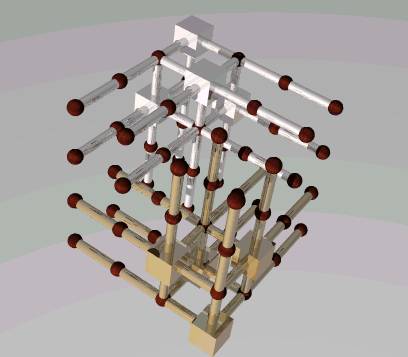
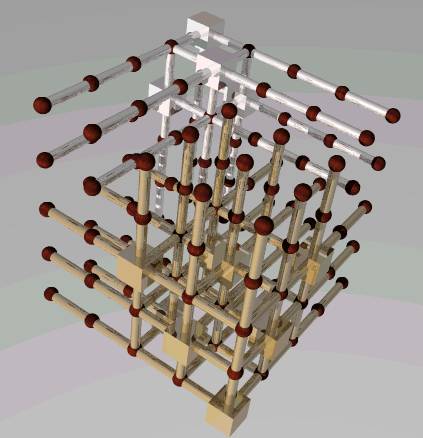
ｎ=2,3,4,5,10 の場合の最小単位立方体数を下表に示す。
選択した単位立方体をシュリンク立方体で、その他の単位立方体を茶色の球で、直線をパイプで示している。

　　　　表１　a-ｂ解答

ｎ	２	３	４	５	１０
最小数	２	５	８	１３	５０
配置図

【上限値と(ｂ)の証明】

n=2〜5はＰＣによる「しらみ潰し」によっても短時間に最小値であることが確認可能である。
ここでは上限値がCeil(n*n/2)あり、n=10の場合、その値：５０個が最小であることを背理法で証明する。

• 定義１：単位立方体を単にセルとよぶ。
  また、選択したセルを「種」とよぶ。
  
  
• 定義２：何れかの面に平行な単一平面上のｎ^２個のセルの集合をを「行」「列」「層」と呼ぶ。
  
  
• 定義３：何れかの辺に平行な単一直線上のセルの集合を考えたとき、１個の「種」もない状態の場合を「空棒」と呼ぶ。
  
  
• 補題１：ある「種」の選び方をＡとするとき、層または列または行を置換した「種」の選び方Ｂが条件を満足するかどうかは、Ａが条件を満足するかどうかと同値である。
  明らかであり証明は略す。
  
  
• 補題２：上限値として　Ceil(n²/2)が設定できる。
  
  ∵図１に示すように、要が立方体である三鼎体の積み木２個で立方体を構成可能である。
  要部の辺長をｐとするとき、要部にｐ^２個の「種」を置くことにより、三鼎体内のセルを全て何れか方向の直線で貫通させることができる。
  その配置はｐが非常に大きい場合にはおよそ、図２に示すような要の立方体の頂点を頂点とする２個（赤・緑）の３角形平面上である。
  精密に式で表わせば、各セルの左下隅頂点の座標を(i,j,k)
  ｛i,j,kは全て区間[0〜p-1]内｝で表すとき、k≡i+j　mod p　　であるセルである。
  
  　よってｎ＝ｐ＋ｑであるとき、「種」の数はｐ^２＋ｑ^２であり、
  この範囲での最小はｐ≒ｑの時であって、
  n=2mなら　2m²，n=2m＋１なら　2m²＋2m＋１である。
  
  これはCeil(x)関数（xを下回らない整数）を用いることにより
  Ceil(n²/2)で一括して表わすことができる。

図１　三鼎体の組み合わせ	図２　要部内の種の配置

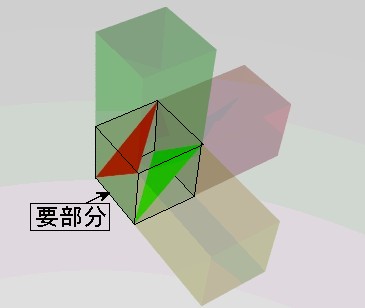☆（ｂ）ｎ＝１０の証明

• 補題２によりｎ＝１０の時、多くとも「種」は５０個で可能である。
  （表１参照)
  
  
• 仮に４９個で可能であったとする。
  このとき、何れかの層で「種」が４個以下のものが必ず存在する。
  
  ４個の場合、補題１により行列を入れ替えると一般性を失わずに下図３−１、か３−２の状態に変換できる。
  また、３個以下の層があったり、４個が狭い範囲に存在する場合は図３−１等の状態である。
  各図における黄色の範囲のセルはその層の「種」からは線を貫通させ得ない。
  即ち、他の層の「種」からの直線を貫通させなければならず、黄色領域のセルの数だけ他の層に「種」が必要である。
  よって、図３−１の状態では黄色部分だけで既に「種」が４９個必要である。
  
  図３−２の状態では使用済みは４６個で、後３個で赤の領域の他の９層（７２セル）をカバーしなければならない。
  しかし１個の「種」でカバーできるセルは、最大でもこの赤領域においては
  層９セル＋行２セル＋列１セル＝１２セルであり、３個では７２セルに対して不足である。
  
  図３−３の状態では、使用済みの「種」は４０個になる。
  あと９個の「種」でカバーすべきセルは、
  赤領域の層９×空棒１２＝１０８セルと、
  青領域の領域２×（層９×列６×行４−黄色領域用３６個×行４）＝１４４セル
  の合計２５２セルである。
  
  一方、残りの９層内において１個の「種」がカバーできるセルの数は最大２７である。
  ２７×９＝２４３であって２５２に対して不足である。
  
  
• よってｎ＝１０の場合の「種」の数は５０個が最小である。　

図３−１	図３−２	図３−３

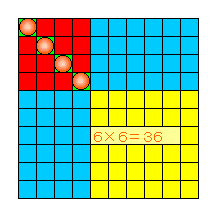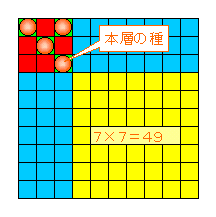
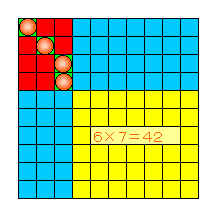
【c （偶数）】　

ｎが偶数の時　２ｍ^２　である。　
ここでｎ＝２ｍ

　∵（ｂ）の証明と同様、「種」の数が２ｍ^２−１で可能であったとする。
すると、これらをうまく分散させても、少なくとも１層は「種」の数がｍ個未満である。

　従って上図黄色相当部分は　ｐ×ｑ　（ｐ、ｑ≧ｍ＋１）であり、[赤＋緑]の部分をカバーするのに使用できる「種」の数は
２ｍ^２−１−ｐ×ｑである。

一方[赤＋緑]の部分は（２ｍ−ｐ）×（２ｍ−ｑ）である。

その差を計算すると　１＋２（ｐ−ｍ）（ｑーｍ）であってｐ、ｑの範囲からその差≧３である。

　つまり少なくとも３本の空棒が[赤＋緑]領域に存在している。
一本の空棒に着目したとき、その２ｍセルを全てカバーするには、その空棒を含む行又は列上の「種」を２ｍ個にしなければならない。
層方向に射影したとき、空棒を除くセルは２ｍ−４個以下である。
従って、最低４個の「種」が射影セル上で重複しなければならない。
このことは、この空棒を含まない別の行または列に空棒が４個追加されることを意味する。
この操作は際限が無くしばらく倍倍ゲームである。
領域が有限であることから、いずれ既に重複した「種」により２ｍ個丁度にすることに寄与する行か列に戻ってくる。
この場合は、新たに追加された空棒を埋めるために必要な新空棒は必ず４個ではなく、最低１個である。
いずれにしても追加する必要があり、終わりがない。

即ち[赤＋緑]の部分の有限性に反する。

【c （奇数）】　

ｎが奇数の時　２ｍ^２＋２ｍ＋１　である。　
ここでｎ＝２ｍ＋１

　∵（ｂ）の証明と同様、「種」の数が２ｍ^２＋２ｍで可能であったとする。
すると、これらをうまく分散させても、少なくとも１層は「種」の数がｍ個未満である。
　従って上図黄色相当部分は　ｐ×ｑ　（ｐ、ｑ≧ｍ＋１）であり、[赤＋緑]の部分をカバーするのに使用できる「種」の数は
２ｍ^２＋２ｍ−ｐ×ｑである。

一方[赤＋緑]の部分は（２ｍ＋１−ｐ）×（２ｍ＋１−ｑ）である。

その差を計算すると　（１＋（２ｐ−２ｍ−１）（２ｑー２ｍ−１））／２であって
ｐ、ｑの範囲からその差≧１である。

　つまり少なくとも１本の空棒が[赤＋緑]領域に存在している。
一本の空棒に着目したとき、その２ｍ＋１セルを全てカバーするには、その空棒を含む行又は列上の「種」を２ｍ＋１個にしなければならない。
層方向に射影したとき、空棒を除くセルは２ｍ−２個以下である。
従って、最低３個の「種」が射影セル上で重複しなければならない。
このことは、この空棒を含まない別の行または列に空棒が３個追加されることを意味する。
この操作は際限が無くしばらく倍倍ゲームである。
領域が有限であることから、いずれ既に重複した「種」により２ｍ＋１個丁度にすることに寄与する行か列に戻ってくる。

　以下偶数と同様であり、両者をまとめると、一般に先に示した上限値が最小値であるといえる。
　即ち　　「種」の数の最小値はCeil(n²/2)である。

【感想】

ＢＢＳでPOV-Rayが話題になったので久しぶりに使ってみました。
自分でいうのも変ですが、問題同様よくできていて、綺麗なＣＧが描け、感心します。

　『高校生からの挑戦状Part25』へ

　数学の部屋へもどる