◆愛知県 YMOjisan さんからの解答。
【問題1】
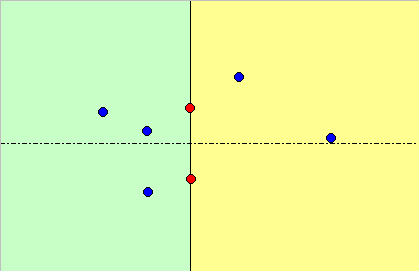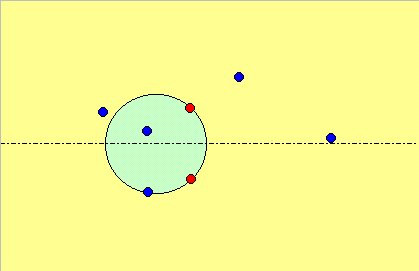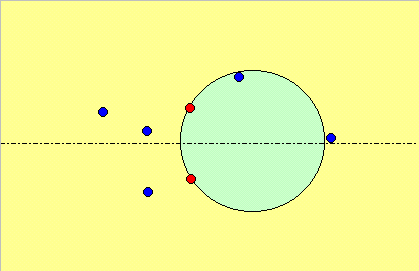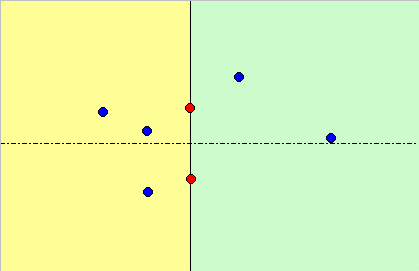
特定の2点(下図赤点)をとおり、中心xが−∞から+∞まで移動する円の内部(緑領域)と外部(黄色領域)にある点(青点)の数の差を
f(x)=内部の点の数-外部の点の数 とする。
なお、点が円上にあるときは0個と数える。
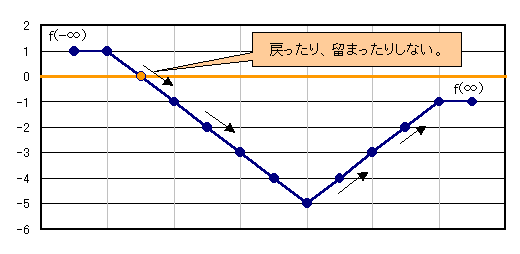
このとき下図から分かるようにf(-∞)=-f(∞)≠0である。なぜなら、
(1)−∞と+∞では領域がいれ代わっている。
(2)青点の個数は2n-1であり、如何なる3点も直線上にないから、左側内部の点の個数をaとすると
f(-∞)=a-(2n-1-a)=2(a-n)+1≠0である。奇数でも有る。
また、如何なる4点も円上にないので、f(x)は整数上において連続であり、かつ点を通過するごとに2変化し、
f(-∞)が奇数値であるので、偶数値は必ず通過する。
よって、偶数値である0になるf(x)の解は必ず奇数個である。
(連続関数の性質より)
ところで、特定の2点の選び方は2n+1C2=(2n+1)nとおりあり、偶奇性はnに一致する。
一方、円は3点により決定されているので、一つの円は3重に計数される。
よって、
良い円の数×3={(特定の2点に対するf(x)=0の個数)を(2n+1)n個足したもの}
であり、nと良い円の数の偶奇性は一致する。

【問題2:存在】
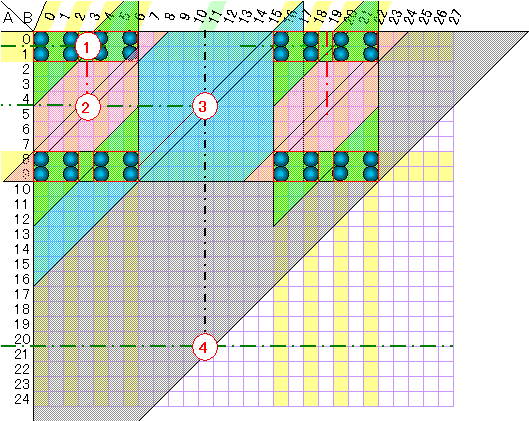
たとえば、Aの部分集合として {0、1}、Bの部分集合として {0、2}とすると下図における緑色の三角形の部分が確定する。
すなわち0〜3までの値に対して和がその値になる組が、1組(青〇)ずつ対応している。
ここで重要なのは、青〇の存在する矩形領域(赤□)において青〇の存在が上下対称であることである。
次に、下図〇1を中心に180度緑△を回転対称コピーする。
青〇の存在が上下対称であったので、この拡張はAの要素として矛盾を起こさず、
問題の条件を満足しつつ、Bの要素を拡大({0、2、4、6})することが可能である。
このようにして得られた桃色△における青〇の存在パターンは必ず左右対称である。
よって下図〇2を中心に180度回転対称コピーすれば、同様にAの集合を拡大({0、1、8、9})できる。
(空色△になる)
以後〇3、〇4、・・・を中心に拡大することが可能であり、数学的帰納法によりA,Bを無限集合にすることが可能である。
【問題2:倍数】
0=0+0の一通りであるから0はA,B両集合に必ず含まれる。
また、1=1+0=0+1であるので、1がA,B何れかに含まれなければならない。
一般性を失わず、Aが1を含み、Bは含まないとする。
このとき本問題は、BがK>1の倍数のみで構成されていることを示すことと等価である。
いまBの0の次の要素をKとする。
このときAは少なくとも0〜K-1を要素として含まなければならない。
そしてこれら部分集合のみで0〜2K-1を和として唯一の組み合わせで表すことが可能であり、一方2Kは表わせない。
2Kを表す方法として、Aの要素として2Kを採用する方法と、Bの要素として2Kを採用する2方法のみが、和が重複しないためには、可能である。
Bの要素として採用するとそれはKの倍数であり、反例にはならない。
B側を連続して採用しつづける場合それは、3K,4K・・・であり、無限に反例は得られない。
一般に、B側にKの倍数でないもの(nK+α)が存在するA、Bの集合があると仮定すると、nK はBの要素ではない。
なぜなら、Aの0〜2K-1とBのnKのどれかで(nK+α)を表わせるからである。
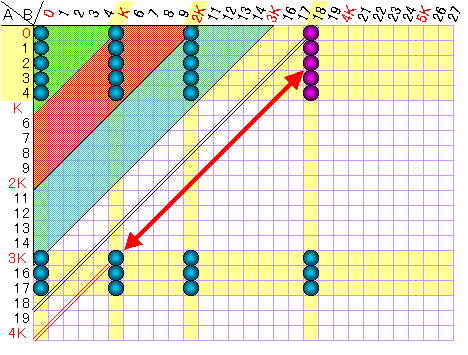
(下図はK=5 n=3 α=3 の場合)
従って、和としてnKを表すためには、Aの集合にnKが必要である。
ところが下図に示すように、Aの0〜K-1と(nK+α)により表わせる数値と、AのnKとBのKにより表わせる数値に重複するものが発生する。
よってBはKの倍数で構成されなければならない。
【感想】
本問題の1は新鮮でした。
グラフ理論かと思いきや、順列組み合わせ+関数の性質でかつシンプルであり、とても良い問題と感じました。
(なお、part19の方の問題1が延々と解けず、こちらに飛んだ次第です。)”