『高校生からの挑戦状Part19』解答

◆愛知県　Y.M.Ojisan さんからの解答。

【問題２】

辺長１の正方形をＳ、辺長１/２未満の正方形をＱとする。
また長さ(√2)/2をｄとする。

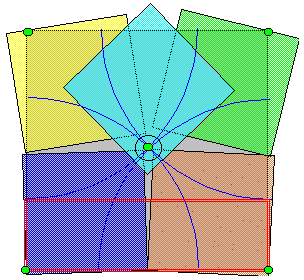
（１）Ｓの頂点及び重心の５点（下図緑点）の距離はｄである。
一方Ｑの対角長はｄ未満であるので、各緑点専属のＱが１個ずつ存在する。



（２）Ｓの周囲の長さの合計は４である。
一方Ｑに含まれる直角Ｌ型の折れ線の長さの最長は、Ｌ型がＱの２辺になった場合であり、１未満である。

従って、Ａの周囲をＱ４個だけで覆うことはできない。
即ち第５のＱ、つまり重心をカバーしているＱは少なくとも何れかの辺上に存在する。
（上図空色Ｑ）

（３）よって、上辺をカバーする３個のＱから届くことの無い、
上図下方の２重赤線で囲まれた長方形[１×（１−ｄ）]が存在し、これを２個のＱで覆えなければならない。

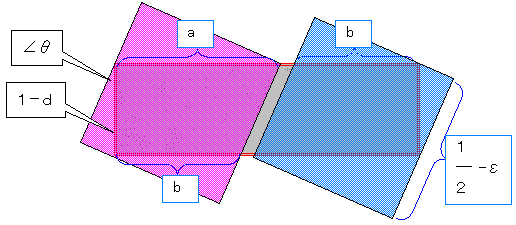
（４）しかし、計算すると下図におけるa+bが最も長くなる下図のような配置でも
a+b＜1であるため、長方形をＱ２個で覆うことはできない。
よってＳをＱ５個で覆うことはできない。

（計算）

a=(1/2-ε)/cos(θ)
(1-d)sin(θ)+b*cos(θ)=1/2-ε
より a+b=(1-2*ε)*cosec(θ)+(1-d)*tan(θ) ：これは下に凸な関数であり最大値は領域の境界である。

θ＝０においてはＱの性質よりa+b=1-2ε＜１である。

もう一方の境界では　(1-d)cos(θ)+（1/2-ε）*tan(θ)=1/2-εが成立し、
ε=0でも　計算するとθ＜0.43920589より　a+b＜0.96726＜1である。

◆東京都　鳥居 さんからの解答。

【問題１】

各桁の数が 0 か 1 の m 桁の数からなる集合 A を考える。

A＝{a|a＝

m-1 Σ i=0

bi10i; bi＝0,1}

A の要素数は 2^m である。
k＜2^m となるように m を定めると、A の中に法 k の下における剰余が等しくなるような２個以上の要素からなる組が必ず存在する。
その組にある２つの要素を a₁,a₂ (a₁＞a₂) とする。
a₁−a₂ は k の倍数であり、その各桁の数は以下の可能性がある。

a1	a2	a1−a2
0	0	0 または 9
1	0	1 または 0
0	1	9 または 8
1	1	0 または 9

よって、a₁−a₂ の各桁の数は 0,1,8,9 の高々４種類である。
2^m-1≦k＜2^m となるように m を定めると、
a₁−a₂ が最大になる可能性は 1.11…×10^m-1 である。

log の底を 2 とすると、以下の不等式が成り立つ。
a₁−a₂≦1.11…×10^m-1＜(10/9)10^m-1＝(10/9)2^{(m-1)log 10}≦(10/9)k^{log 10}
k≧2 であるから、10/9＝2^log(10/9)≦k^log(10/9) が成り立つ。
よって、a₁−a₂＜k^{log 10＋log(10/9)}＝k^log(100/9) となる。
log(100/9)＝3.4739…＜4 であるから、k⁴ 未満の k の倍数で、各桁の数が 0,1,8,9 の４種類以下で構成されるものがあることが示される。

手の付けどころが難しくて、面白い問題と思いました。
k を場合分けしたらどうか…、有名な定理を使ったらどうか…と思考をめぐらせましたが、４種類の数をどれにするかに着目したところ、道が開けました。

　『高校生からの挑戦状Part19』へ

　数学の部屋へもどる