『高校生からの挑戦状Part13』解答

◆広島県　清川　育男 さんからの解答。

十進べーシック(1000桁モード)で求めてみました。
規則性がつかめません。

 FOR J=1 TO 9
    PRINT J;
    PRINT ")"
    LET  Z=0
    FOR I=1 TO 1000
       LET  X$=STR$(2^I)
       IF VAL(MID$(X$,1,1))=J THEN
          LET  Z=Z+1
          REM PRINT USING "#####":I
       END IF
    NEXT I
    PRINT USING "###":Z;
    PRINT "個"
 NEXT J
 END

◆宮城県　甘泉法師 さんからの解答。

（方針）

4 ≦

2p 10q

＜ 5

自然対数をとって
0 ≦ （ｐ‐2）ln2 - ｑ ln10 ＜ ln5‐2ln2

この式を満たす負でない整数ｑが1〜1000のｐに対していくつ存在するかはコンピュータで確かめられます。

◆宮城県　甘泉法師 さんからの解答。

（方針２）

最高位がMがくるものに一般化すると

M ≦

2p 10q

＜ M+1

２を底とする対数をとって
β≦ ｐ - ｑ α ＜γ

ここで
α＝log₂10
β＝log ₂M
γ＝log₂ (M+1) .

よってｘｙ平面上の４つの直線

ｙ ＝ αｘ + β 直線上を含む
ｙ ＝ αｘ + γ 直線上は含まない
ｙ ＝ １ 直線上を含む
ｙ ＝ 1000 直線上を含む

で囲まれた部分にある格子点の数が答。
数は作図で求められる。

（方針２追加）

おおよその数の検討をつけます。
線で囲まれた平行四辺形部分の面積と中の格子点の数はほぼ等しい。

よって

平行四辺形の底辺の長さ

γ-β α

= log

10

(1 +

1 M

) が最高位がMである数の割合の極限。

M 割合

1 0.301029996
2 0.176091259
3 0.124938737
4 0.096910013
5 0.079181246
6 0.06694679
7 0.057991947
8 0.051152522
9 0.045757491

清川さんの結果とよく一致します。

【コメント】

底は２でなくても任意の正の実数P、
指数kは１〜１０００でなくても任意の続く自然数(N個)で、
P^kをE進法であらわした最大の桁の数がMである割合は

N→∞の極限でlog

E

(1 +

1 M

) となることがわかります。

かなり一般的な結果ですね。

◆愛知県　Y.M.Ojisan さんからの解答。

◆　答え　９７個

『2ⁿ/10^m』の解答より

２10 １０００

＝１．０２４　　　　−−−（１）

(

２10 １０００

)

98

＝１０．２１９...＜１．０２４×１０　　　−−−（２）

５×８＝４０　−−−（３）

を利用する。

２^ＰをＰ mod 10 で１０組に分類し　
mod値が　 {2 5 8 1 4 7 0 3 6 9 12=2}である順に、
Ｐ＝{2 5 8 11 14 17 20 23 26 29 32}が同一行になるように始まりをずらしてならべる。下図参照。

Group{２}の系列は４から始まり（１）より１．０２４を公比として徐々に増加し何れ５を以上になるが、この時（３）により次のGroup{5}の系列が必ず４を先頭とする数になる。

以下繰り返しで一巡したら、Group{12=2}の系列に戻るが、
この時３×１０＝３０乗分位置が少ない側にずれる。
また、（２）より１０００乗までなら一巡で終わる。
従って９７個である。

　説明より、下図を見る方がその構造が容易に理解できる。
実際の数値を計算（適当に１０ⁿで約分）しているが、９７個を出すには一部を除き不用である。



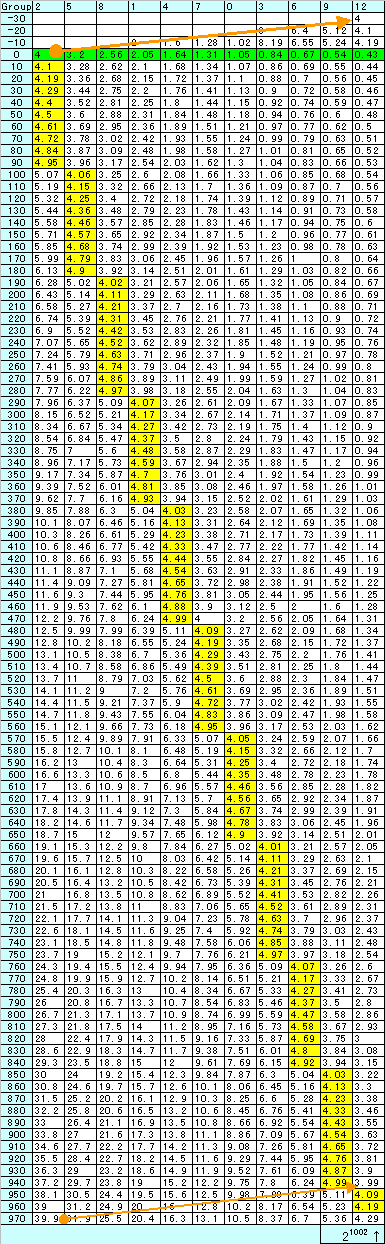
【感想】
　２^ｎの特殊な部分を利用した大変綺麗な問題だと思いました。

◆大阪府　ゆたか さんからの解答。

対数は常用対数とします。 log2=0.30102…より、
log2⁹⁹⁹=300.7… ， log2¹⁰⁰⁰=301.0…

よって、2⁹⁹⁹は３０１桁、2¹⁰⁰⁰は３０２桁の数です。

今、2⁰，2¹，2²，・・・，2¹⁰⁰⁰を桁数によってグループ分けします。

つまり、
（１桁のグループ）１，２，４，８
（２桁のグループ）１６，３２，６４
（３桁のグループ）１２８，２５６，５１２
（４桁のグループ）１０２４，２０４８，４０９６，８１９２

　　　　・
　　　　・
　　　　・

（３０１桁のグループ）・・・，2⁹⁹⁸，2⁹⁹⁹
（３０２桁のグループ）2¹⁰⁰⁰

となります。

各グループにおいて最高位の数字の推移を調べると、次のことがわかります。

（�T）グループの先頭の数の最高位は「１」である。

（�U）「１」のあとは、直前の項の２倍か２倍＋１の数が最高位となる。
（理由）直前の数を２倍したときに下位で繰上りがなければ最高位は２倍になり、
　　　　繰上りがあれば最高位は２倍＋１となる。

（�V）最高位が「５」以上になると、そのグループの末項となる。

これらのことから、グループにおける最高位の数字の推移は次のいずれかのパターンになります。

１−２−４−８
１−２−４−９
１−２−５
１−３−６
１−３−７

よって、グループの項数は３または４となります。
さらに、最高位が「４」の数は項数が４のグループにのみ現れることがわかります。

そこで、３０１桁のグループまでで、項数が４のグループ数をＸとし、項数が３のグループ数をＹとします。
グループは３０１個ありますから、
　　　Ｘ＋Ｙ＝３０１　・・・(1)

また、2⁰から2⁹⁹⁹までの項の総数は１０００だから
（2¹⁰⁰⁰は次のグループ）、

　　　４Ｘ＋３Ｙ＝１０００　・・・(2)

(1)，(2)を解くと、Ｘ＝９７，Ｙ＝２０４となります。
最高位が「４」の数の個数はＸに等しいので９７個が答えです。

この解法は最高位が「４」の数にしか通用しませんね。
しかし、例えば次のようなこともわかります。

• 最高位が「８」または「９」である数は「４」である数と同数現れる
• 最高位が「６」または「７」である数は「３」である数と同数現れる
• 最高位が「４」または「５」である数は「２」である数と同数現れる

◆京都府　大空風成 さんからの解答。

X=２¹⁰⁰⁰として、両辺の底を10とする対数（常用対数として以下底を省略）をとると、
logX=1000log2=301.0・・・　（log2=0.3010・・・だから）
よって　X=10^{301.0・・・}
ゆえに　10³⁰¹＜２¹⁰⁰⁰＜10³⁰²　だから、２¹⁰⁰⁰は302桁の数で ある。
また、Y=２⁹⁹⁹として同様に、
logY=999log2=300.6・・・　
よって　Y=10^{300.6・・・}
ゆえに　10³⁰⁰＜２⁹⁹⁹＜10³⁰¹となるから、２⁹⁹⁹は301桁の数で ある。

２ⁿの最高位が1である数を2倍すると、最高位が2、3のいずれかの数になる。
２ⁿの最高 位が2、3である数を2倍すると、最高位が4または5、6、7のいずれかの数になる。
２ⁿの最高位が4で ある数を2倍すると、最高位が8、9のいずれかの数になる。
２ⁿの最高位が5、6、7、8、9である数を2倍すると、一桁増えて最高位が1の数になる。
したがって、２ⁿの同じ桁数の数は、
最高位が1の数が１つ、2、3のいずれかの数が1つ、5、6、7、8、9のいずれかの数が1つ、
つまり、最高位が4以外の数になる場合が必ず3つあることが分かる。
さらに、２⁹⁹⁹は301桁、２¹⁰⁰⁰は302桁だから、２¹⁰⁰⁰の最高位は1であること も分かる。

以上のことより、 ２ⁿの2桁以上301桁以下の数の中にある最高位が4以外の数の個数は、
(301-2+1)×3=900（個）
である。これに、1桁の数の２¹、２³、302桁の数の２¹⁰⁰⁰を加えると、903個に なる。
よって、最高位が4の数は、1000-903=97

（答）　97個

（別解）

　『高校生からの挑戦状Part13』へ

　数学の部屋へもどる