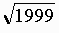と小数点以下７７桁まで一致しています。
◆富山県 N.C さんからの解答。
取り敢えず、プログラムを使って自明でない解
（x=1,y=0）を一組見つけました。
x=4027701399389138208695911951306886478800プログラムは
y= 90084665203202024260494303744425250249
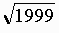の近似分数 x/y を連分数を用いて生成し、その中で与えられた条件を満たすものを探します。ちなみに、
|
4027701399389138208695911951306886478800 ―――――――――――――――――――――――― 90084665203202024260494303744425250249 |
は、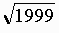と小数点以下７７桁まで一致しています。
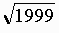を連分数展開したときの循環節の長さが８４と非常に長く、計算ループを８４回、回したときのものが上の解答です。
◆福岡県 まさゆき さんからの解答。
ｘ2−１９９９ｙ2＝１
(ｘ＋１)(ｘ−１)＝１９９９ｙ2 ・・［１］
１９９９は素数であるので
ｘ＋１、ｘ−１どちらかは１９９９を因数にもつ
ここで ｘ＋１＝１９９９ｋのとき
［１］に代入
１９９９ｋ(１９９９ｋ−２)＝１９９９ｙ2
ｋ(１９９９ｋ−２)＝ｙ2
ここでこの式が成立するためには、
１９９９ｋ−２は k を因数にもつ
よってｋ＝−２、−１、０、１、２
それぞれｋに代入したとき題意を満たすのは
ｋ＝０のみである
よって ｘ＝−１、ｙ＝０
また ｘ−１＝１９９９ｋにおいても同様にして
ｋ＝０であり、ｘ＝１、ｙ＝０
よって（ｘ、ｙ）＝（−１、０）（１、０）
◆富山県 N.C さんからの解答。
この問題について、参考書をひっくり返してみました。
インターネット上で、「ペル方程式」というキーワードで検索をかけても沢山の情報が得られるようです．
正整数ｍに対して、
不定方程式ｘ2−ｍｙ2＝±１
（およびｘ2−ｍｙ2＝±４）は、整数論の分野で重要なもので、ペル方程式と言われています．
以下，ｘ2−ｍｙ2＝１の場合を考えます。
（Ｘ、Ｙ）が解ならば
（−Ｘ、Ｙ）（Ｘ、−Ｙ）（−Ｘ、−Ｙ）も解なので、必要ならば符号を付け替えて、正の整数の場合のみ考えます。
Ａ）ｍが平方数でない場合，正整数解は存在する。
北村泰一「整数論入門」（槇書店数学選書）には、ディリクレの引出し論法（鳩ノ巣論法）による証明があります。
高木貞治「初頭整数論講義」（共立出版）では、連分数論による証明と、イデアル論による証明とがあります。
Ｂ）（ｘ1,ｙ1）が最小の正整数解のとき、
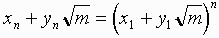
となるように整数(ｘn,ｙn)を定めると、正整数解全体は
｛(ｘ1,ｙ1),(ｘ2,ｙ2),(ｘ3,ｙ3),..｝で与えられる。
Ｃ）連分数展開を用いて、正整数解をすべて求められる．
高木貞治「初頭整数論講義」（共立出版）、
河田敬義「数論１，２，３」（岩波講座基礎数学）などに証明がある。
これらの本は、証明に必要な予備知識があちこちに散在していて、理解するのには根気がいる。
このＣ）から、連分数を用いて一番最初に見つかる
ｘ2−1999ｙ2＝１の正整数解
ｘ1＝4027701399389138208695911951306886478800
ｙ1＝ 90084665203202024260494303744425250249
は、最小の正整数解であることが判ります．
正整数解全体は、これからＢ）の式で求めることができます。
なかなか大変な結果になりました。