――――

◆東京都 千葉 英伸 さんからの解答。
【問題1】
1から1999までの1000個の奇数のうち2数の和で2000をつくるとすると、
その組み合わせは、以下の500通り。
(1,1999)
(3,1997)
(5,1995)
・・・・
(997,1003)
(999,1001)
しかも、この中には考えている1から1999までの奇数がすべて1回ずつ現れる。
さて、1から1999までの1000個の奇数から任意に500個を取ったとする。
この中に上記500通りの組み合わせのうち1組でも入っていれば問題は解決なので、どの組も、2数ともには入っていないとする。
今、500個の奇数を取ったのだから、その取り方は上記500組すべてから、2数のどちらか片方を取っていることになる。
従って、さらに任意に1個(全部で501個)取れば、500組のうちのどれかの組が2数とも含まれる。
【問題2】
| まず、半径 |
1 ――――  | の円 |
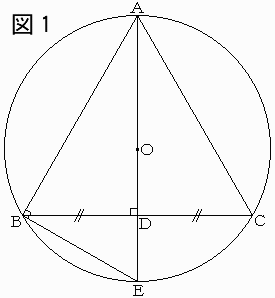
図1から、∠BAE=30゚なので、
| AB:AE=AB: |
2 ――――  | = :2 :2 |
∴AB=1
| つまり、問題の半径 |
1 ――――  | の円 |
そこで、1辺の長さ44の正三角形を次図2のように1辺の長さが1の小さな正三角形に分割する。
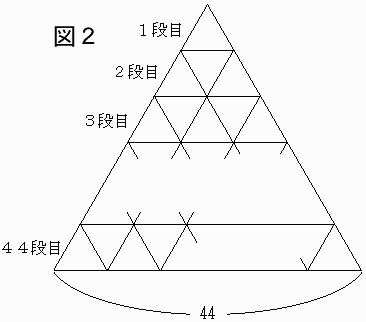
1辺の長さ1の小正三角形が全部でいくつあるか数えてみる。
1段目=1個
2段目=3個
3段目=5個
・・・・・・
n段目=2n−1個
となるので、
(n段目までの合計)
=Σ(2n−1)
| =2 |
n(n+1) ―――― 2 | −n |
全部で44段あるので、小正三角形は
全部で44×44=1936個ある。
さて、1辺の長さ44の正三角形の中に1999個の点があるとすると、上で考えた小三角形は1936個しかないのだから、必ずどれかの小正三角形には複数の点が含まれる。
(*)より、この小正三角形(1辺の長さが1)は
| 半径 |
1 ――――  | の円に内接するので、 |
【問題2の考察】
たぶん、出題者の一平さんは上記のような証明を意図していたのだと思います。
細かいことですが、この証明でも題意を満たす点の個数は
1936+1個あれば十分です。
(1999年にひっかけて1999個の点にしたのだと思いますが)
実はこの問題、さらに厳密に考えれば点の個数はもっともっと少なくてよいことが、以下のように証明できます。
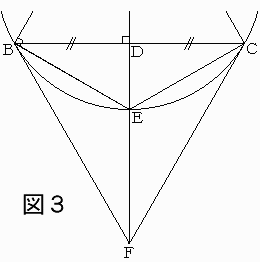
図1を利用して、辺BCを1辺とする下向きの正三角形BFCを考える。(図3)
△BECと△FECで、
∠BED=∠CED=60゚なので、
∠BEC=∠FEC=120゚
また、∠BCF=60゚なので、
∠BCE=∠FCE=30゚
辺ECは共通なので
△BEC≡△FEC
同様にして、
△BEC≡△FEB
このことから何がいえるかというと、図2で、下向き(▽の向き)の小正三角形は、その周りの3つの上向き(△の向き)の小正三角形の外接円によって覆われてしまうということがいえる。
従って、全体の大きな正三角形自身が、すべての上向き(△の向き)の小正三角形の外接円で覆われる。
そこで、上向きの小正三角形を数えてみると、n段目にn個あるので、
| (n段目までの合計)= |
1 ―― 2 | n(n+1) |
44段では、全部で
44×(44+1)/2=990個ある。
つまり、1辺44の正三角形は、
| 990個の半径 |
1 ――――  | の円 |
従って、991個の点があれば、少なくともどれか1つの円内に2個以上の点が存在することになる。
題意を満たす点の個数は991個で十分ということになる。
一般に、nを自然数とすると、1辺nの正三角形の中に、
|
1 ―― 2 | n(n+1)+1個の点 |
| 2点を含む半径 |
1 ――――  | の円が描ける。 |