◆広島県 清川 育男 さんからの解答。
【問題1】
4乗であるのでχ1〜χ14は負でない整数としてもよい。
74=2401 であるから、
0≦χ1〜χ14≦6 でなければならない。
04=0
14=1
24=16
34=81
44=256
54=625
64=1296
χ14〜χ144は
0,1,16,81,256,625,1296のいずれかでなければならない。
0がA個、1がB個、16がC個、81がD個、
256がE個、625がF個、1296がG個とする。
A,B,C,D,E,F,Gは負でない整数。
A+B+C+D+E+F+G=14 ........................(1)
B+16C+81D+256E+625F+1296G=1999...........(2)
14元4次不定方程式と同値になると思います。
A=0 のとき
1+16+81+256+625+1296=2275>1999
したがって、A≠0でなければならない。
16+81+256+625+1296=2274>1999
B≠0でなければならない。
81+256+625+1296=2258>1999
C≠0でなければならない。
256+625+1296=2177>1999
D≠0でなければならない。
したがって、3<A<11でなければならない。
また0≦E<8,
0≦F<4,
0≦G<2でなければならない。
1)G=1のとき
A+B+C+D+E+F=13
B+16C+81D+256E+625F=703
イ)F=1のとき
A+B+C+D+E=12
B+16C+81D+256E=78
D=0,
E=0,
5<A<11
A+B+C=12
B+16C=78
15C=66+A
C=5,A=9,B=-2
これは不適。
したがってF≠1である。
ロ)F=0のとき
4<A<11
A+B+C+D+E=13.......................(3)
B+16C+81D+256E=703.................(4)
(4)-(3)
15C+80D+255E=690+A
5(3C+16D+51E)=690+A
i) A=10
B+C+D+E=3
これは矛盾である。
ii) A=5
B+C+D+E=8........................(5)
(4)-(5)
15C+80D+255=695
3C+16D+51E=139..................(6)
3(C+17E)+16D=139..................(7)
D=1
C+17E=41
E=2,C=9 C+D+E=13
これは矛盾。
D=4
C+17E=25
E=1,C=8
C+D+E=13
これは矛盾。
D=7
C+17E=9
これは矛盾。
イ)、ロ)からG≠1である。
2)G=0のとき
4<A<11
A+B+C+D+E+F=14......................(8)
B+16C+81D+256E+625F=1999............(9)
(9)-(8)
15C+80D+255E+624F=1985+A
5(3C+16D+51E)+624F=1985+A
イ)F=1のとき
A+B+C+D+E=13
5(3C+16D+51E)=1361+A
i)A=4
B+C+D+E=9
3C+16D+51E=273
3(C+17E)+16D=273
D=3
B+C+E=6
C+17E=75
16E=69+B
E,Bは存在しない。
D=6
B+C+E=3
B=C=E=1
1+16+81*6+625=1128
これは不適。
ロ)F=2
A+B+C+D+E=12
5(3C+16D+51E)=735+A
A=5
3C+16D+51E=148
B+C+D+E=7
3(C+17E)+16D=148
D=1
C+17E=44
B+C+E=6
16E=38+B
E,Bは存在しない。
ハ)F=3
A+B+C+D+E=12
5(3C+16D+51E=113+A
A=2
3C+16D+51E=23
C,D,Eは存在しない。
A=7
3C+16D+51E=24
C,D,Eは存在しない。
イ)、ロ)、ハ)からG≠0である。
1)、2)から(1)(2)を満たすA,B,C,D,E,F,Gは存在しない。
ゆえにχ1〜χ14は存在しない。
7元1次不定方程式に還元するのだろうと思いますが、それが解を持つための必要十分条件でスマートに解決する方法があるのでしょうね。
網が破れているかもしれません。
◆広島県 清川 育男 さんからの解答。
【問題1】
4乗であるから簡単にするために、
χ1〜χ14は負でない整数と考えてもよい。
74=2401 であるから、
χ1〜χ14は0〜6でなければならない。
04=0,
14=1,
24=16,
34=81,
44=256,
54=625,
64=1296
χ14〜χ14は
0,1,16,81,256,1296のいずれかである。
ここで16の剰余で考える。右辺=1999≡15 (mod 16)
0≡0 (mod 16)
1≡1 (mod 16)
16≡0 (mod 16)
81≡1 (mod 16)
256≡0 (mod 16)
625≡1 (mod 16)
1296≡0 (mod 16)
したがって、16の剰余で考えると、
χ14〜χ144は0か1である。
仮にχ14〜χ144の16の剰余がすべて1としても、
1×14=14≠15
ゆえに左辺の16の剰余は15になることはない。
したがって、χ1〜χ14の整数解は存在しない。
◆東京都 千葉 英伸 さんからの解答。
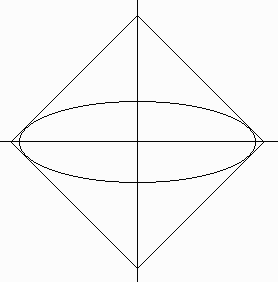
【問題2】

与えられた楕円が、一般の
|
χ2 ―――― a2 | + |
y2 ―――― b2 | =1・・・(1) |
の場合で計算してみる。
正方形の1辺の方程式を
y=χ+m・・・(2)
として、(1)に代入し、χで整理すると、
(a2+b2)χ2+2a2mχ+a2m2−a2b2=0(1)と(2)は接しているので、この方程式は重解を持つ。よって、
(a2m)2−(a2+b2)(a2m2−a2b2)=0
これを展開すると、おもしろいように整理されて、
m2=a2+b2
という結果が得られる。
従って正方形の1辺の長さは
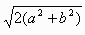
ちなみに、円の場合には
a=b=r なので、
円に外接する正方形の1辺の長さは2r、つまり直径と等しくなる。
この問題の場合には1辺の長さは
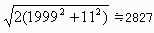
となる。