◆静岡県 ヨッシー さんからの解答。
問題の996点は998点として解答します。
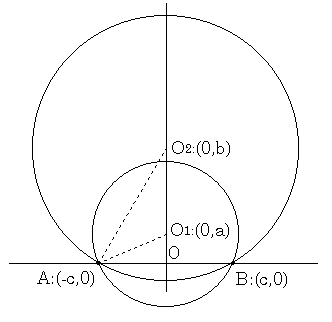
図のように、x軸上に2点A(-c,0)、B(c,0) があります。
このとき、2点A、Bを通る円の中心は、y軸上にありますが、そういう円について、次のことがいえます。
中心の座標が、O1:(0,a),O2:(0,b) で、2点A,Bを通る2つの円
x2+(y-a)2=a2+c2・・・(1)
x2+(y-b)2=b2+c2・・・(2)
を考えます。ただしa<b。
このとき、円(1)上の点で、y>0である点はすべて円(2)の内部に存在します。
(予備証明)
円(1)上の点
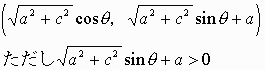
を(2)の左辺に代入して、
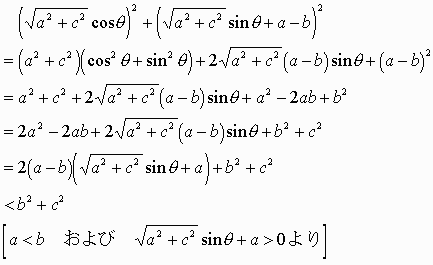
よって、円(1)上の点で、y>0である点はすべて円(2)の内部に含まれる。
(予備証明終わり)
(本証明)
平面上に1999個の点があるとき、
ある2点を通る直線を引いて、他の1997個の点が、その直線について、同じ側にあるような、2点A,Bを選ぶことはできる。
この2点A,Bと、他の1997個の点のうちの1個を通る円は必ず存在して、それらの中心は、2点A,Bを結ぶ線分の垂直二等分線上にあり、すべて異なる点となる。
これらの点を、2点を通る直線に対して、点が存在しない側から順に、
O1,O2,O3・・・O1997 と番号をつけ、それに対応する1997個の点(円周上の点でA,B以外の点)を
C1,C2,C3・・・C1997 とする。
予備証明より、O999 を中心とする円に対し、
3点A,B,C999 は円周上に、
C1,C2,C3・・・C998 の998点は内部に、
C1000・・・C1997 の998点は外部に存在する。
(本証明終わり)